A string x is accepted if running the machine on input x considering all paths including the use of εtransitions puts the machine into one of the accepting states Formally. Clearly A L and A L accept the same language L.

Nfa Of Regular Language L Ab Ba Geeksforgeeks
The answer is basically in the question you link but to make it explicit.

. Assuming R ϵ then R describes the language ϵ and to prove that it is regular we shall construct a NFA M QΣ δ q F that accepts this language. Consider the languages L1 and L2 a. The minimum pumping length for the language 1010 is.
Each regular expression can be systematically translated into an NFA. Design an NFA to recognize the following language where fabcg L. If an NFA has n states then you can always construct an equivalent DFA True False using at most 2n states.
Construct an NFA that accepts the same language using the construction algorithm given in Lemma 155 of the textbook. Let M be an NFA with a single accepting state show how to construct the 5-tuple for a new NFA say N with LN xy x LM and y LM. Following the above-mentioned rules -NFA of Regular Language L b ba is to be constructed.
If a language is regular then it is described by a RE. We obtain this NFA by defining Q q q the start state F q and δq a State diagram of M. The pumping lemma can be used to show that a language is regular.
Since both the terms are connected by sign there will be two paths coming out of the first node. Assuming R then R describes the language and to prove that it is regular we construct an NFA M QΣ δ. Using deterministic finite automata DFAs.
Union of 4 and 6 More Text Exercises. You cannot build an NFA to recognize the language 0n1n for n 0. NFA stands for non-deterministic finite automata.
Using a closure definition involving union concate-nation and. Show activity on this post. Using nondeterministic finite automata NFAs.
It is easy to construct an NFA than DFA for a given regular language. Although not all the states will be there. Construct the NFA for ba.
The language LA accepted by NFA is defined as. Which one of the following represents L1 L2 U L1. The idea here is to make two copies of the NFA linking the accepting state of the first to the.
Based on the work for Questions 1 and 2 design an NFA to recognize each of the following languages. Construct the NFA for bab. A Consider the regular language described by the regular expression R 0 U 110 u 1.
The finite automata are called NFA when there exist many paths for specific input from the current state to the next state. Concatenation of 5 and b. For an example let L be any regular language.
NFA is defined in the same way as DFA. L b ba has two terms. Since youll know how to convert languages to NFA in this sequel I dispense with drawing the NFAs for these REsbut you are.
Thats what well try to do here. Convert N into a GNFA Generalized NFA called G that. Construct an NFA that accepts the same language using the construction algorithm given in Lemma 155 of the textbook.
Create a new kind of machine a GNFA Generalized NFA that has the same power as a NFA and that is suited to proving Lemma 160. The machine accepts only if it ends with. LA w δ q0 w F That is LA is the set of strings w in such that δ q0 w.
Regular Language L has an NFA call it N. Every NFA is not DFA but each NFA can be translated into DFA. Construct the NFA for abab bab.
Concatenation of 3 and b. After that if it sees at least one b it can accept. X Σis accepted by M if.
The first term is fairly easy to construct. Suppose that C is a language recognized by some NFA M ie C LM. Each regular language can be compactly described using a regular expression.
By problem 3 on Homework 2 we then know there is another DFA D that recognizes the language LD. Transitions ε-NFA Accepting a string. Indicates an empty language.
B Consider the DFA M 9192930189193 where 8 is defined in the table below. Final state of the DFA is set of subset of NFA states such that. Assuming this is correct how would the complement of L N look like.
For each set and for each input symbol a in This above is the formula to fill subset table. We give six definitions of the regular languages. DFAs NFAs Regular Languages The family of regular languages is the simplest yet inter-esting family of languages.
This will be the transition table for the DFA. Concatenation of with any other language is. B Consider the DFA M q9293 018993 where 8 is defined in the table below.
L N x Σ x mustnt include aba and x mustnt end with ab I have tried several different words and I couldnt find any word that breaks my language L N. The language L of the NFA N should look like this. Here is a table of REs and the languages they denote.
First thing to do is where ever there is the. Complete subset construction nfa to dfa. However the automaton obtained.
If it sees a b before an a it crashes. Show that the language of construct NFA is indeed LN as specified. L1 L2 U L1 Result of L1 L2 is.
Since every NFA has an equivalent DFA Theorem 139 there is a DFA D such that LD LM C. Concatenation of b and a. Regular languages and finite automata.
A Consider the regular language described by the regular expression R 0U 1100 U 1. Nondeterministic Finite Automata with ε. Although when filling by hand it is clearly visible.
Proof idea - For each RL convert its NFA into an equivalent RE. Wcontains an even number of as or contains the pattern aag Answer. L a n b m n 0 m 0 and n m Pumping Lemma.
Is this language L over the alphabet a b regular. The second term is to be drawn following the second rule of construction. No there is no nice expression since anything can happen.
It can see any number of b but after the initial run of a it can never again see two a in a row. Construct the NFA for abab. Lets say its accepted by NFA A L.
Your NFA loops in q0 accepting any number of a until it sees at least one a.
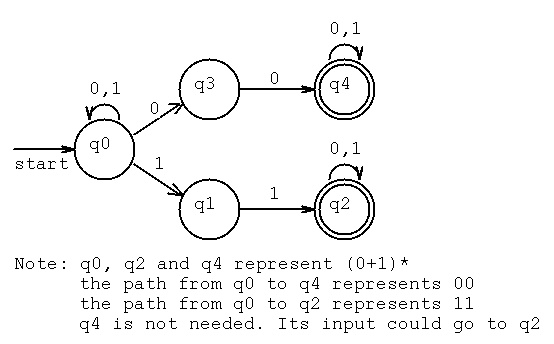
Cmsc 451 Lecture 4 Nondeterministic Finite Automata Nfa

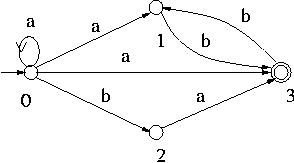
Nfa Of Regular Language L 0 1 00 11 And L B Ba Geeksforgeeks
0 Comments